Interest Rate Parity (IRP) Theory

Interest Rate Parity (IPR) theory is used to analyze the relationship between at the spot rate and a corresponding forward (future) rate of currencies.

The IPR theory states interest rate differentials between two different currencies will be reflected in the premium or discount for the forward exchange rate on the foreign currency if there is no arbitrage - the activity of buying shares or currency in one financial market and selling it at a profit in another.

The theory further states size of the forward premium or discount on a foreign currency should be equal to the interest rate differentials between the countries in comparison.

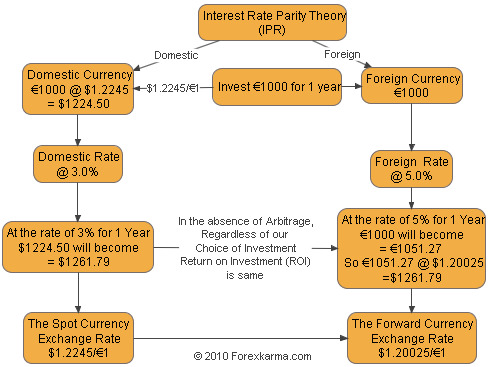Interest Rate Parity Flowchart

Examples

For our illustration purpose consider investing € 1000 for 1 year.

We'll consider two investment cases viz:

Case I: Domestic Investment

In the U.S.A., consider the spot exchange rate of $1.2245/€ 1.

So we can exchange our € 1000 @ $1.2245 = $1224.50

Now we can invest $1224.50 @ 3.0% for 1 year which yields $1261.79 at the end of the year.

Case II: Foreign Investment

Likewise we can invest € 1000 in a foreign European market, say at the rate of 5.0% for 1 year.

But we buy forward 1 year to lock in the future exchange rate at
$1.20025/€ 1 since we need to convert our € 1000 back to the domestic currency, i.e. the U.S. Dollar.

So € 1000 @ of 5.0% for 1 year = € 1051.27

Then we can convert € 1051.27 @ $1.20025 = $1261.79

Thus, in the absence of arbitrage, the Return on Investment (RoI) is same regardless of our choice of investment method.

There are two types of IRP.

1. Covered Interest Rate Parity (CIRP)

Covered Interest Rate theory states that exchange rate forward premiums (discounts) offset interest rate differentials between two sovereigns.

In another words, covered interest rate theory holds that interest rate differentials between two countries are offset by the spot/forward currency premiums as otherwise investors could earn a pure arbitrage profit.

Covered Interest Rate Examples

Assume Google Inc., the U.S. based multi-national company, needs to pay it's European employees in Euro in a month's time.

Google Inc. can achieve this in several ways viz:

• Buy Euro forward 30 days to lock in the exchange rate. Then Google can invest in dollars for 30 days until it must convert dollars to Euro in a month. This is called covering because now Google Inc. has no exchange rate fluctuation risk.
• Convert dollars to Euro today at spot exchange rate. Invest Euro in a European bond (in Euro) for 30 days (equivalently loan out Euro for 30 days) then pay it's obligation in Euro at the end of the month.

Under this model Google Inc. is sure of the interest rate that it will earn, so it may convert fewer dollars to Euro today as it's Euro will grow via interest earned.

This is also called covering because by converting dollars to Euro at the spot, the risk of exchange rate fluctuation is eliminated.

2. Uncovered Interest Rate Parity (UIP)

Uncovered Interest Rate theory states that expected appreciation (depreciation) of a currency is offset by lower (higher) interest.

Uncovered Interest Rate Example

In the above example of covered interest rate, the other method that Google Inc. can implement is:

• Google Inc. can also invest the money in dollars today and change it for Euro at the end of the month.

This method is uncovered because the exchange rate risks persist in this transaction.

Covered Interest Rate Vs. Uncovered Interest Rate

Recent empirical research has identified that uncovered interest rate parity does not hold, although violations are not as large as previously thought and seems to be currency rather than time horizon dependent.

In contrast, covered interest rate parity is well established in recent decades amongst the OECD economies for short-term instruments. Any apparent deviations are credited to transaction costs.

Implications of Interest Rate Parity Theory

If IRP theory holds then arbitrage in not possible. No matter whether an investor invests in domestic country or foreign country, the rate of return will be the same as if an investor invested in the home country when measured in domestic currency.

If domestic interest rates are less than foreign interest rates, foreign currency must trade at a forward discount to offset any benefit of higher interest rates in foreign country to prevent arbitrage.

If foreign currency does not trade at a forward discount or if the forward discount is not large enough to offset the interest rate advantage of foreign country, arbitrage opportunity exists for domestic investors. So domestic investors can benefit by investing in the foreign market.

If domestic interest rates are more than foreign interest rates, foreign currency must trade at a forward premium to offset any benefit of higher interest rates in domestic country to prevent arbitrage.

If foreign currency does not trade at a forward premium or if the forward premium is not large enough to offset the interest rate advantage of domestic country, arbitrage opportunity exists for foreign investors. So foreign investors can benefit by investing in the domestic market.

Limitations of Interest Rate Parity Model

In recent years the interest rate parity model has shown little proof of working.

In many cases, countries with higher interest rates often experience it's currency appreciate due to higher demands and higher yields and has nothing to do with risk-less arbitrage.