Adaptive Moving Average

Adaptive moving average (AMA), as the name suggests is an adaptation of moving average. It is designed to adapt according to the dynamic market as needed.

Simple moving average (SMA) and its cousins weighted moving averages (WMA) and exponential moving averages (EMA) all work fantastic when the market is trending.

However when the market is range bound they pick up a lot of market noise generating a lot of premature signals.

Moreover, they are all inherently lagging in nature.

In a quest to remedy shortcomings of moving averages, Perry J. Kaufmann, first introduced adaptive moving average in his book The Smarter Trading: Improving Performance in Changing Markets.

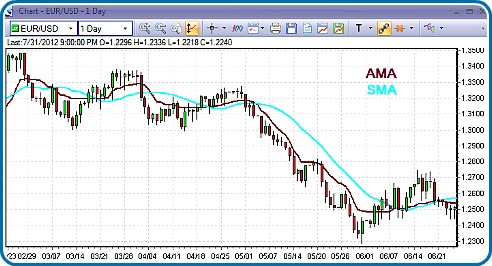20-Day-SMA & AMA In Action

Prior to Mr. Kaufmann's introduction of AMA, traders employed combination of more than a single moving average such as The Double Crossover Method and The Triple Crossover Method.

The reasons behind employing multiple combination of moving averages are based on the following facts:

Fast moving averages, which often consists of shorter time period such as 5-day period performed best when the market is rapidly trending.

Slow moving averages, which often consists of longer time period such as 50-day period performed best when the market is range bound thereby filtering most of the noise in the market.

So the genius in Kaufmann's AMA was a system smart enough to vary its speed according to a combination of market direction and speed.

In another words, when the market is trending, AMA speeds up along with the trend. When the market is range bound and does nothing AMA slows down.

Thus it righteously earns the name "adaptive" as it self adjusts to market direction and speed.

Kaufmann's AMA achieves sense of market direction and speed by incoporating the efficiency ratio.

The Adaptive Moving Average Calculation

Let's do some math but first let's really understand what the efficiency ratio translates to in plain simple language.

By the end of our discussion you will be amazed to discover how Kaufmann ingeniously incorporates efficiency ratio in designing smart system that can adapt to market direction and speed.

Mathematically,

Efficiency Ratio (ER) = Direction / Volatility

Now ratios are used to make comparison between two things.

In our case of finding Efficiency Ratio (ER) we are basically attempting to determine whether the market is directional (trending) or volatile (market noise).

By dividing the directionality by the market noise, the ratio varies between 0 to 1 or simply 0% to 100% such that 0 ≤ ER ≤ 1.

In another words, ER is equal or greater than 0 and ER is equal or smaller than 1.

Determining Price Direction

Price direction can be expressed as the net price change over time.

direction = price - price_n

where,
direction = the current price direction
price = current price (daily close or hourly close)
price_n = the close n-days ago (or n-periods ago)

Determining the Volatility

The best way to express volatiltiy is to calculate the sum of all the day-to-day or hour-to-hour price changes ( each taken as a positive number), over the same n periods.

volatility = sum of absolute value of (price - price_1) over n periods

where,
volatility = today's volatility value
absolute value (positive value of any numbers)
sum = the sum of "value' over n periods

This idea of efficiency ratio is so significant as we will see how one can transform lagging and noise producing SMA to trend catching, and noise filtering adaptive moving average (AMA).

Let's look at to the EMA formula first...

EMA_today = EMA_yesterday + α X (Price_today - EMA_yesterday)

where, α = smoothing constant

Next we will employ our newfound efficiency ratio (ER).

We will change it to smoothing constant and then substitute it for smoothing constant in above formula.

EMA_today = EMA_yesterday + c X (Price_today - EMA_yesterday)

where, c = new smoothing constant that replaces α.

Our above new formula shows that the exponential average gets closer to today's close by percentage, c, of yesterday's gap.

c relates to SMA by the formula,
c = 2/(n-1), where n is the number of days.

AMA = AMA_1 + Smoothing Constant X (Price - AMA_1)